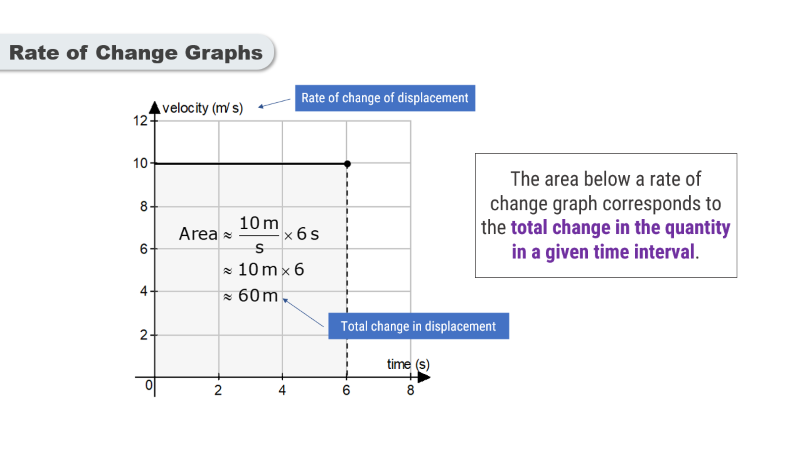
The area beneath a rate of change often represents real-world quantities such as total displacement, energy, accumulated change, or total volume.

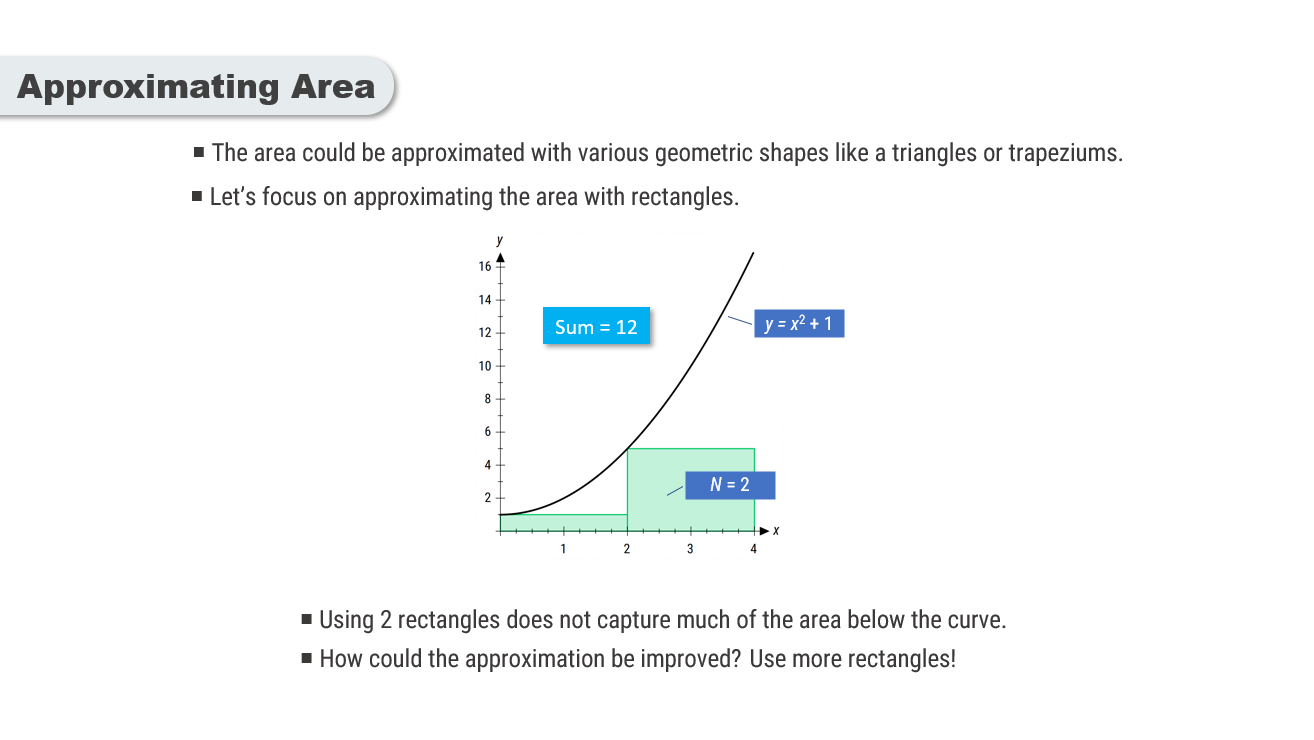
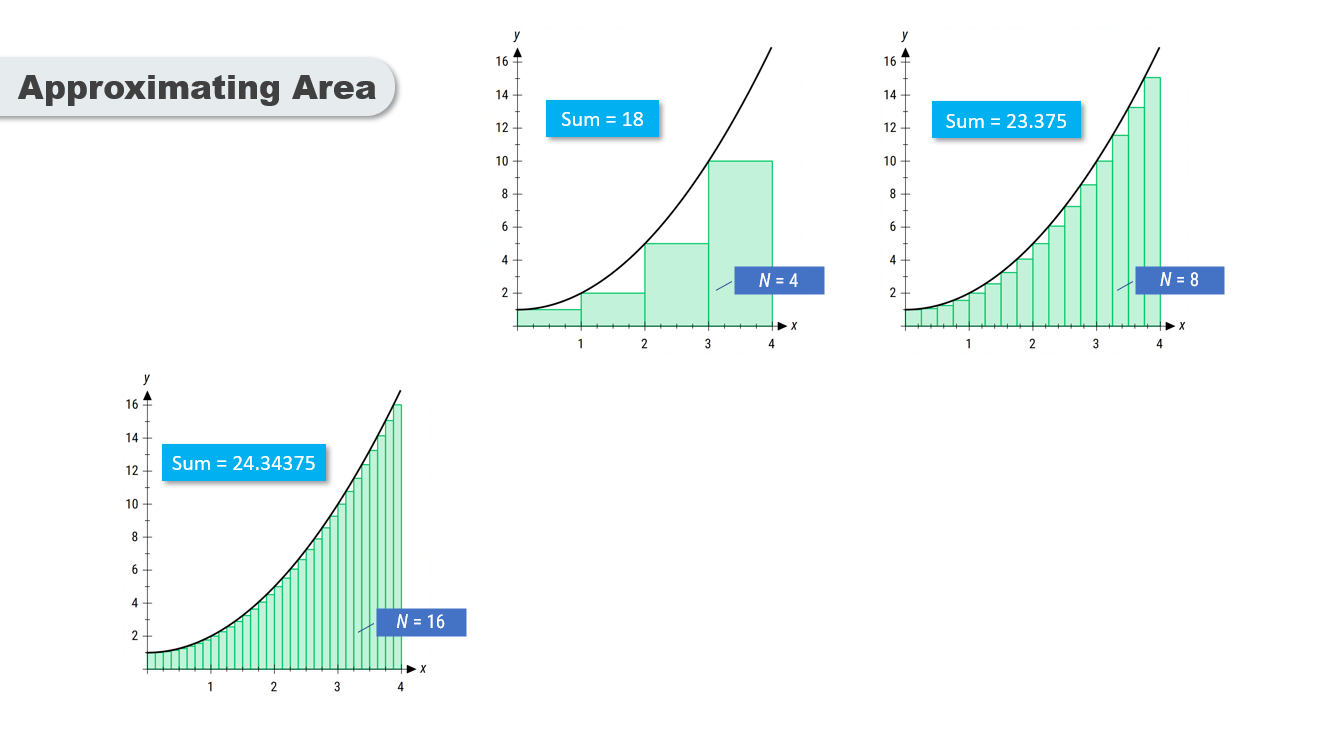
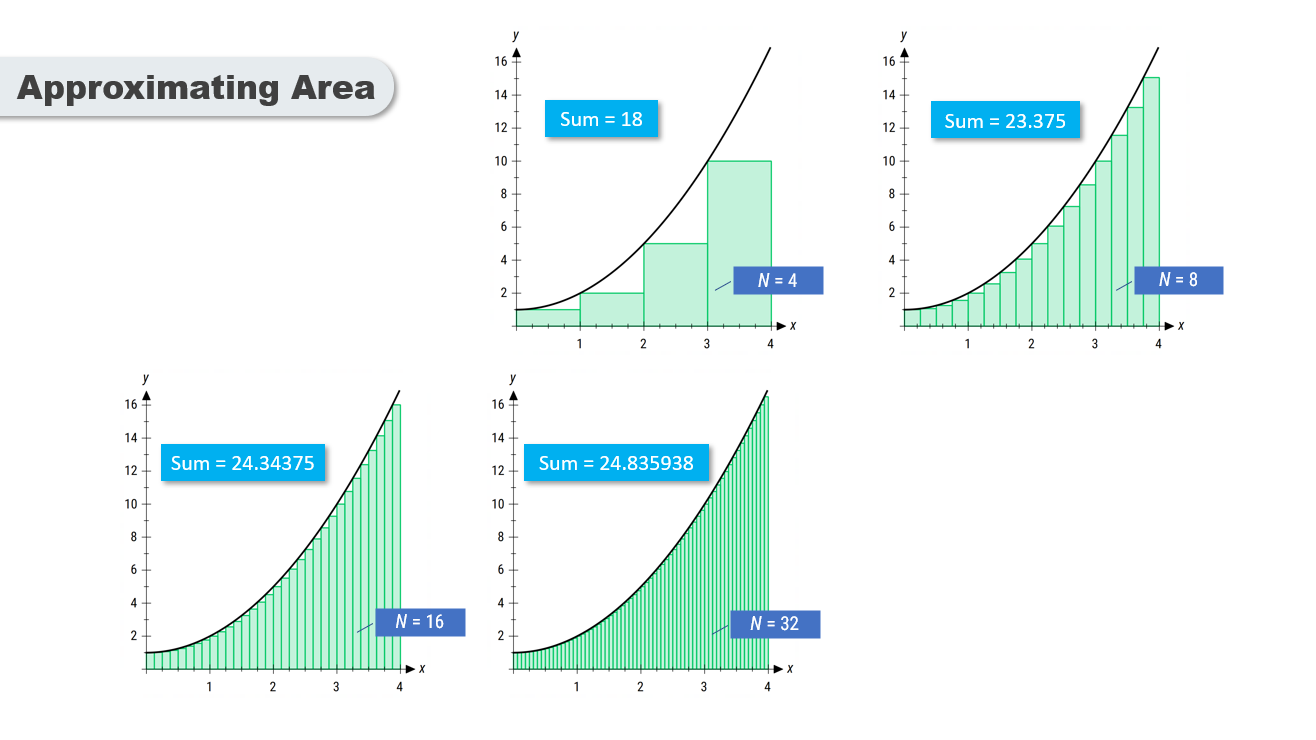
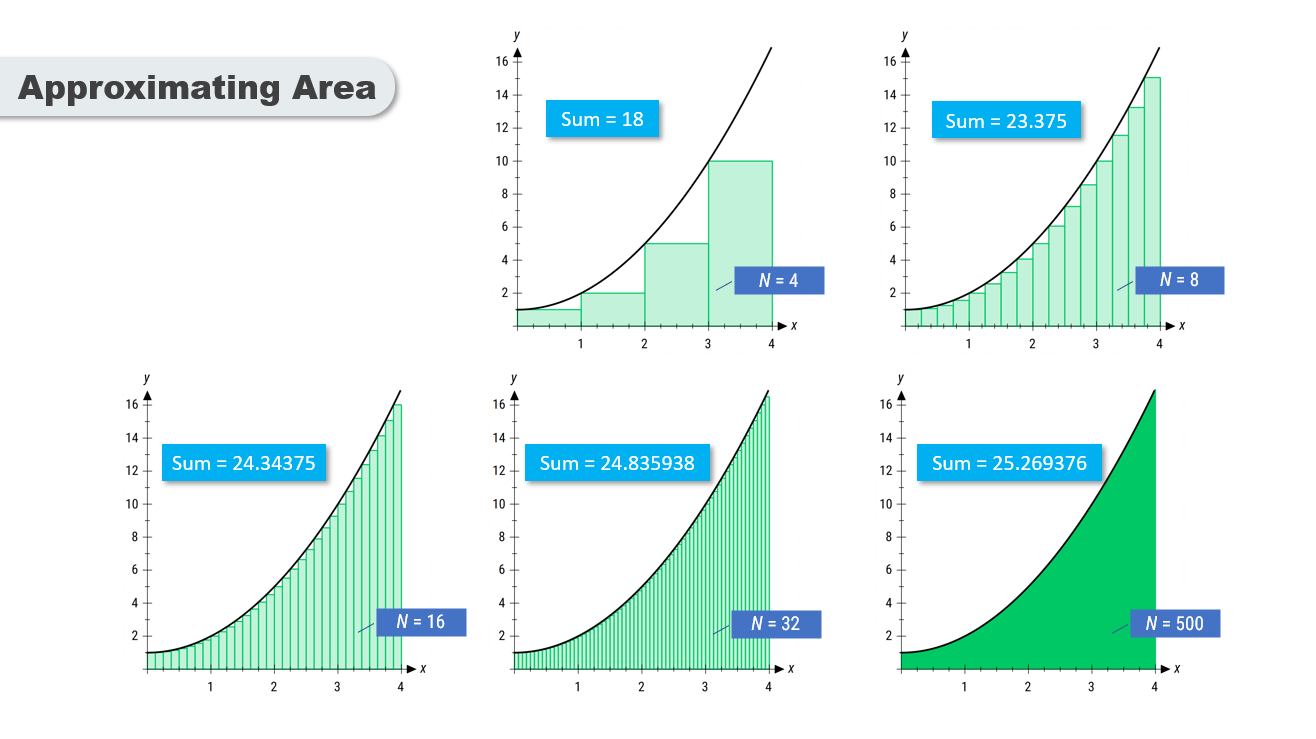
The area under a curved graph can be approximated using geometric shapes such as triangles, trapeziums, or rectangles.
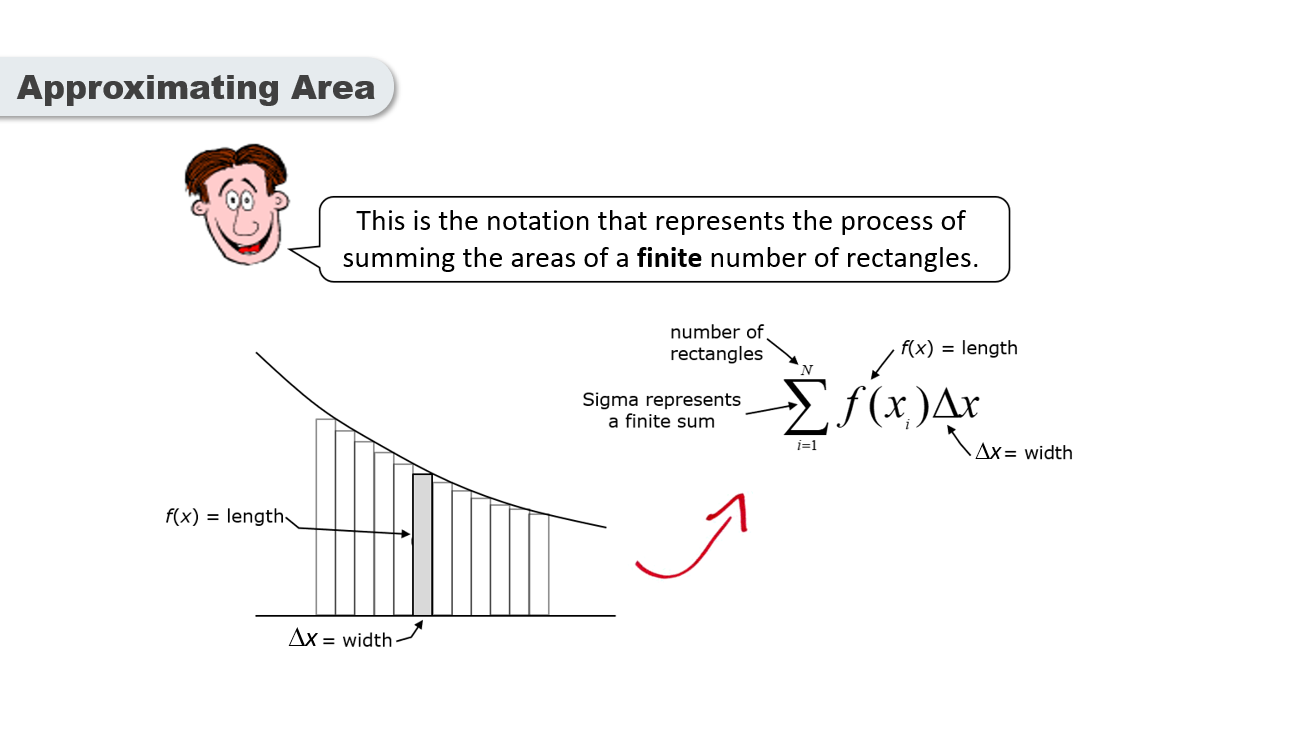
A common method is to divide the area into rectangles and sum their areas to estimate the total.

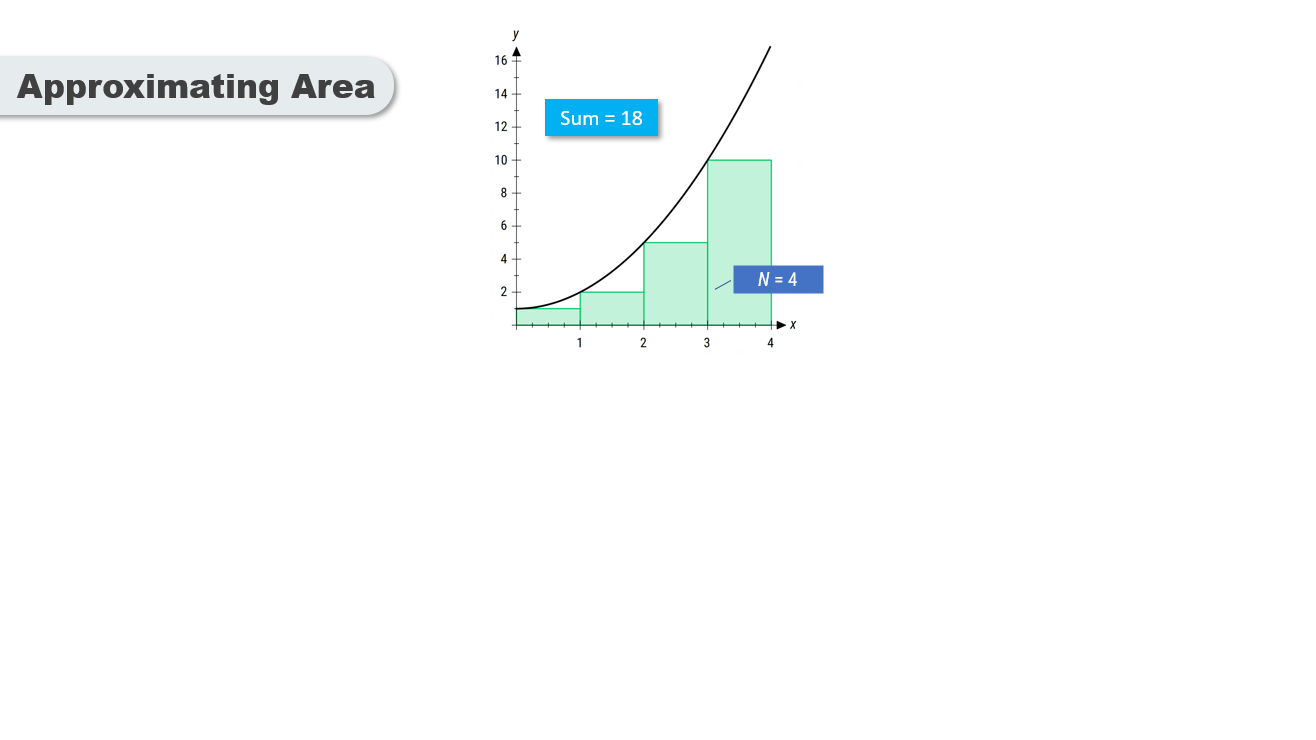
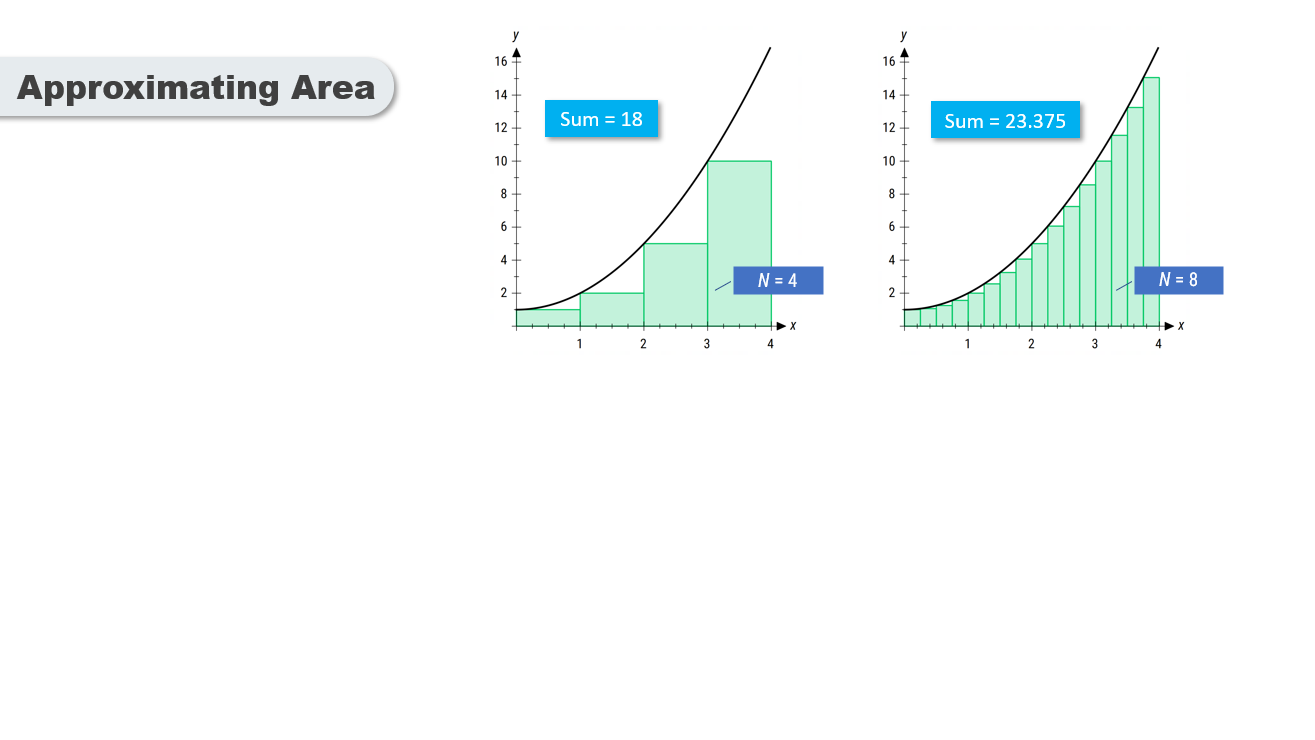
As more rectangles are used, the approximation of the area becomes more accurate.
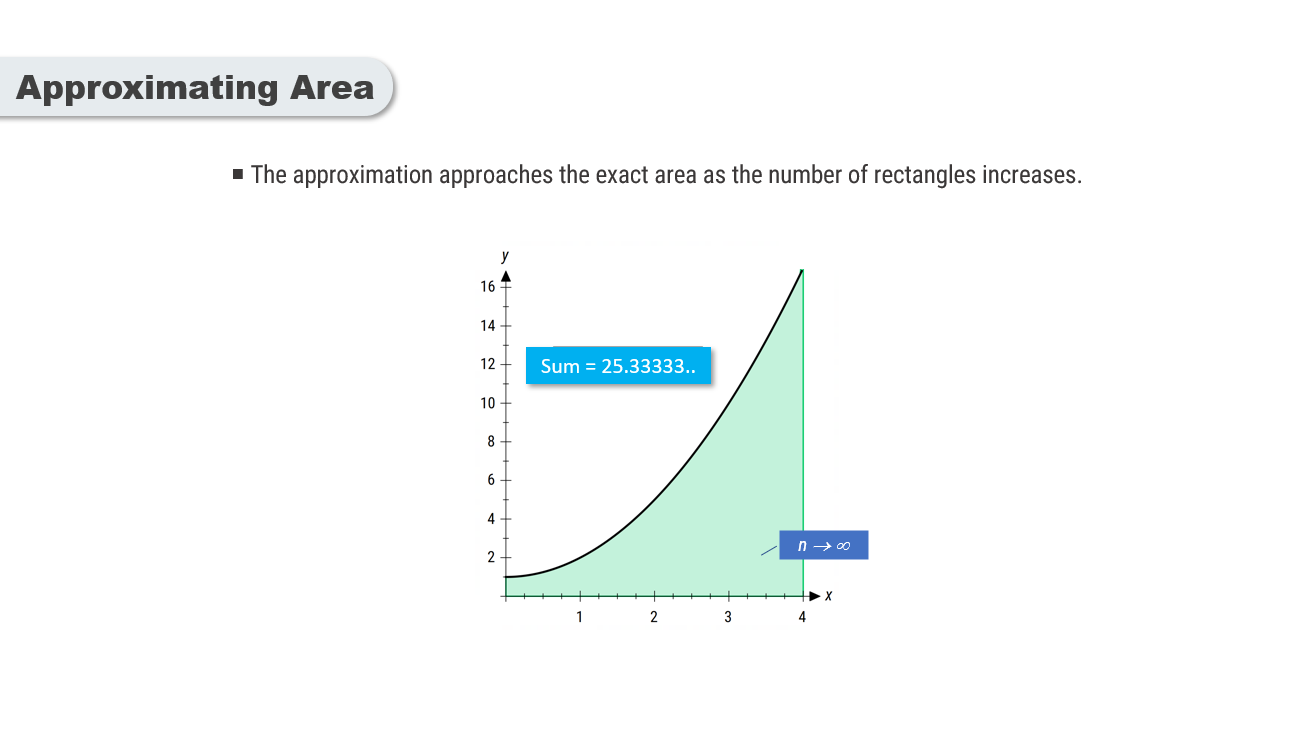
The sum of the rectangles' areas approaches the exact area under the curve as the number of rectangles increases.

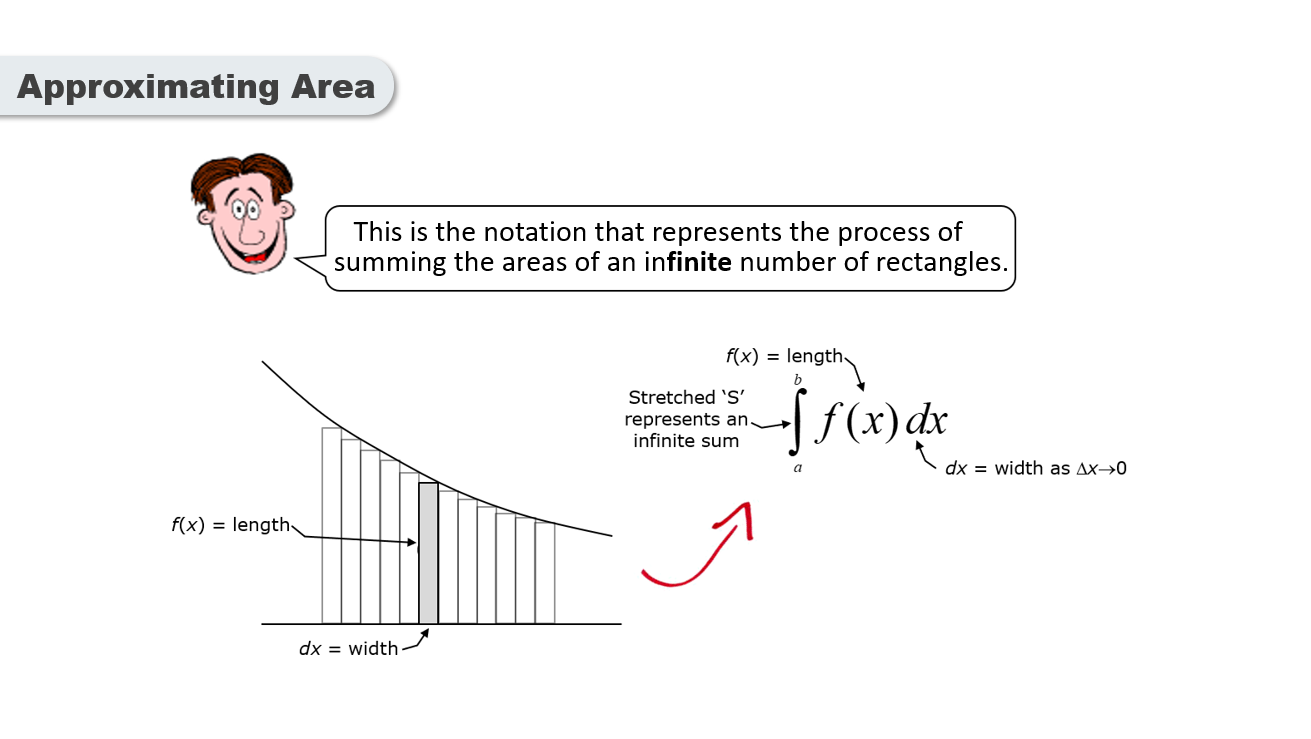
Integration is the mathematical process of summing an infinite number of rectangles to obtain the exact area under a curve.
It generalizes the concept of approximation by taking the limit as the number of rectangles approaches infinity.

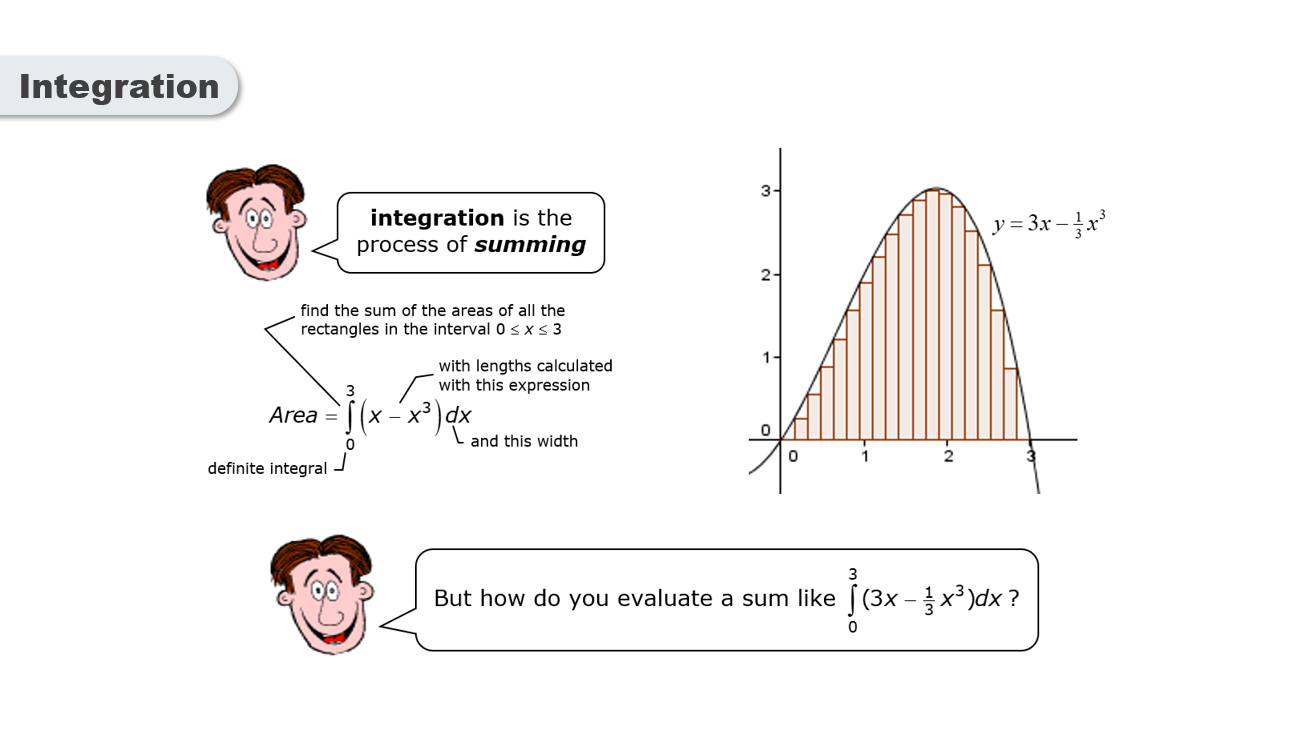
The Fundamental Theorem of Calculus connects differentiation and integration. It states that a definite integral can be evaluated using the antiderivative of the function.
This theorem allows us to compute exact areas under curves without needing to sum infinitely many rectangles.